2023.11.07

データ分析における過剰適合の罠

AIME

本文章は、シグナル&ノイズ天才データアナリストの「予測学」（ネイト・シルバー著）の内容を要約しております。

【中古】シグナル＆ノイズ天才データアナリストの「予測学」／ネイトシルバー【著】，川添節子【訳】，西内啓【解説】

created by Rinker

¥1,573 (2024/12/22 16:25:07時点楽天市場調べ-詳細)

Contents

過剰適合という落とし穴
現実に起こる過剰適合
素晴らしいモデルはノイズを多く含む

過剰適合という落とし穴

統計学では、「過剰適合」というのはノイズをシグナルと間違えることを指します。
例えば、もし私が盗みのボスで、あなたが私の部下だとしましょう。
私があなたに命じたのは、あらゆる状況で有効なダイヤル錠のピッキング方法を見つけることです。
私はあなたに赤、黒、青の3つの錠前を練習用に渡します。

数日後、あなたは「赤なら27-12-31、黒なら44-14-19、青なら10-3-32で開く」という絶対確実な方法を見つけたと報告します。
しかし、これは問題です。
確かにこれら特定の錠は開けられますが、これには応用性がありません。
何も知らない状態でどの錠も開けられるわけではありません。
私が求めていたのは、たとえばピッキングに使えるクリップが存在するか、錠に構造的な欠陥があるのか、そうでなければ番号の組み合わせのコツがあるかのような情報です。
よく使われる番号などです。
あなたの持ってきた解答は問題に対してあまりに限定的です。
これが過剰適合の一例であり、誤った予測へと繋がります。

現実に起こる過剰適合

過剰適合という言葉は、統計モデルが過去の観察結果に過度に合致してしまうことから来ています。
適合度が低すぎるとシグナルが把握できず、適合度が高すぎると実際の構造を理解せずにデータのノイズに合わせてしまいます。
この過ちは現実によく発生します。

想像してみてください。
本物のデータがどのように見えるかが完全に分かっているとします（これは現実ではほぼ不可能ですが）。
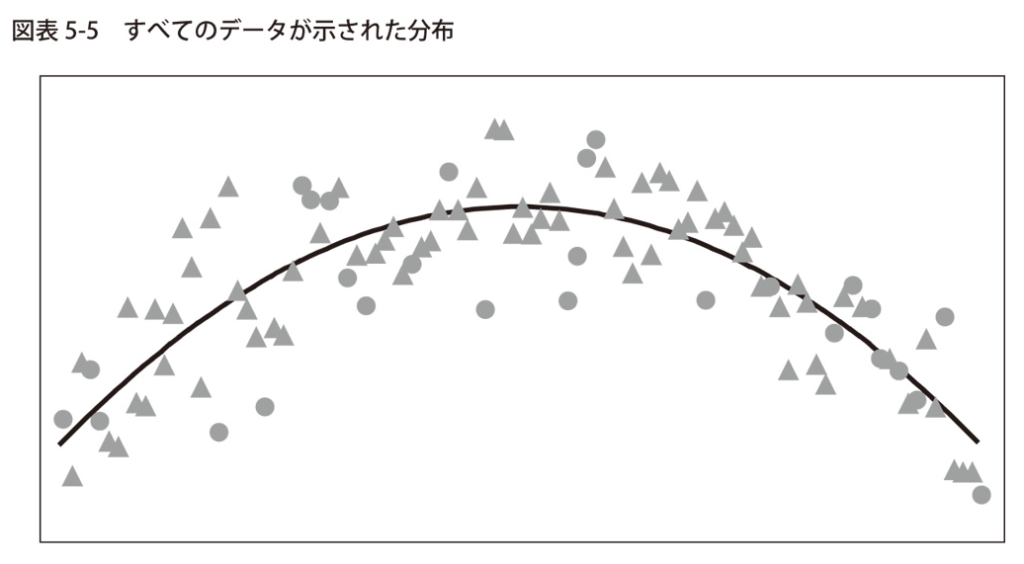
あるデータの分布が中央にピークを持つ滑らかな放物線で示されているとします。
この放物線は例えば野球選手のキャリアの中間に能力のピークがあるエイジング・カーブなどのデータに相当します。
キャリアの初めと終わりは、ピークと比べて見劣りします。

この背後にある関係性は一見して明らかではありません。
個々のデータ点が何かしらの意味を持っていると考えられますので、その背後にあるパターンを我々は推測しなくてはなりません。
これらのデータは環境の影響を受けます。
つまり、そこには有意なシグナルが存在する一方で、無意味なノイズも混在しています。
図表5-5を注意深く観察すると、マークされた100個のマルと三角が点在しているのがわかります。
有意なパターンを見つけ出すことはさほど難しくないはずです。
データがランダムに散らばっている部分もありますが、その分布がある種の曲線に沿っていることははっきりしています。

しかし、もしデータがより限定されたものだったらどうでしょうか。
実際のところ、このようなケースの方がより一般的です。
そして、分析はより複雑になります。
例えば、図表5-6aは図表5-5の100個のデータ点の中からマル印のものだけを抽出したものです。
これらの点をどのように結びつけるべきか、という問題が浮かび上がります。

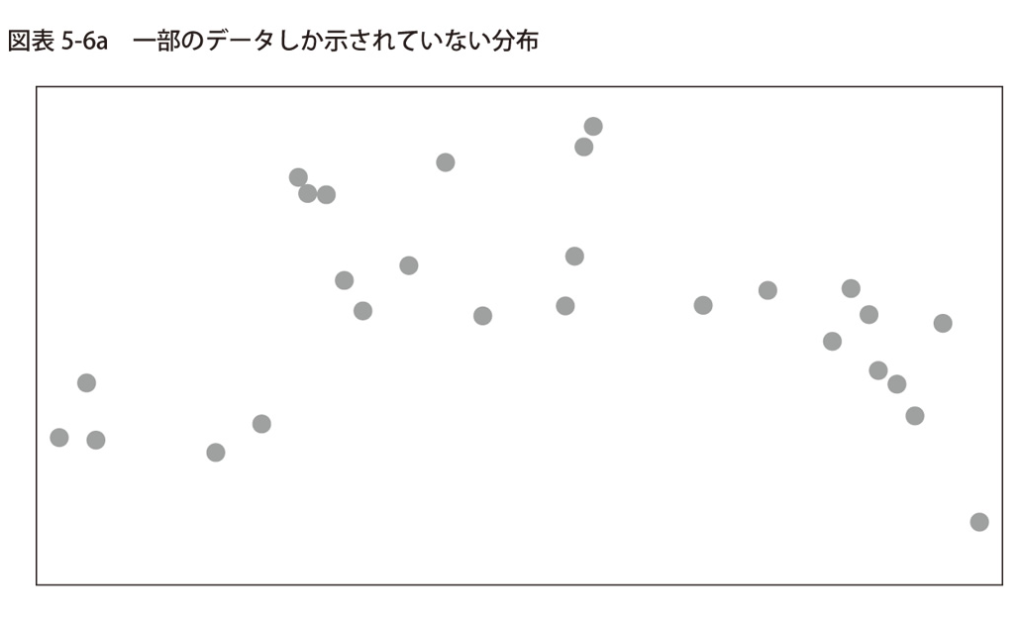
既にあなたは全てのデータがどのように分布しているかを把握しているため、自然と放物線状の曲線を描きたくなるでしょう。
図表5-6bを見ながら、実際に曲線を描いてみると、データの背後にある真の関係性を上手く表現することが可能になります。

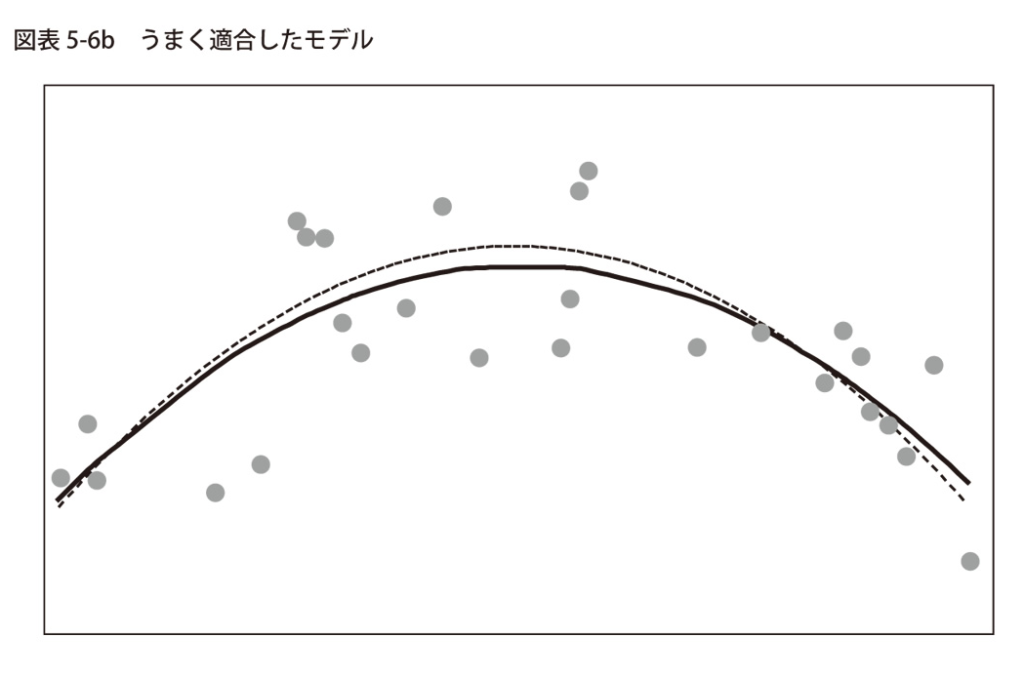
データの全体像を把握していない場合、過度にデータに合わせようとしてしまうことがあります。
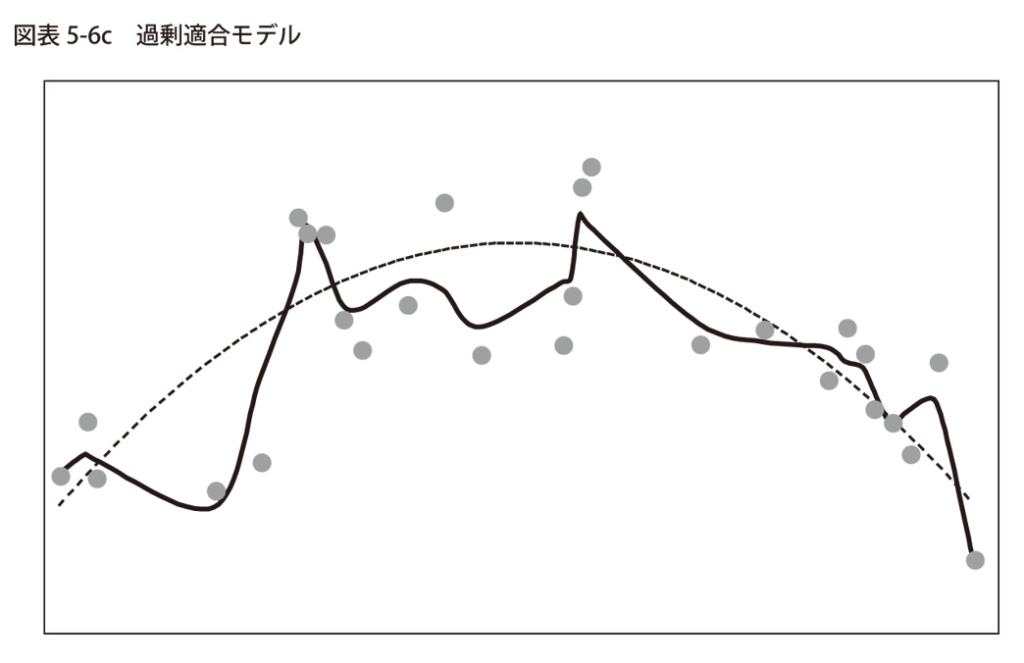
図表5-6cは、その典型的な例を示しています。
これは過剰適合モデルです。
データ点を全て結びつけようとするあまり、遠く離れたデータ点までをも取り込んでしまい、結果として線が複雑になりすぎています。
このようなモデルでは、真の関係性を正確に捉えることができず、予測精度も低下してしまいます。

素晴らしいモデルはノイズを多く含む

あなたがもし全知全能で、常にデータ分布の背後にある構造を見抜くことができるなら、過剰適合のような間違いは容易に避けられるかもしれません。
しかし、実際には、私たちは持っている証拠からのみ推論を立て、帰納的に物事に取り組むしかありません。
データが限られていたり、基本的な関係についての知識が不足していたりすると、過剰適合したモデルを作りがちです。

過剰適合が発生するのは、全ての関係性を理解していないとき、またはそれを気にしないときです。
一つの理由は、多くの統計的テストが過剰適合モデルに高いスコアを与えるからです。
たとえば、あるテストでは過剰適合モデルが85%、もう少し単純なモデルが56%の分布の変動を説明できていると結果が出るかもしれません。
しかし、この高いスコアは、実際にはノイズにまでフィットしてしまっており、現実を正しく表しているわけではありません。

多くの予測者がこの問題を見過ごすことがあります。
利用可能な統計的手法が豊富であるにも関わらず、それを誤用すれば、子どもが雲を見て動物の形に見立てるのと変わりません。
これはもはや科学とは言えません。
ジョン・フォン・ノイマンはこの問題について言及しており、「4つのパラメーターで象を描くことができ、5つあればその鼻を動かして見せることができる」と述べています。

過剰適合は実際のところ、実際のモデルよりも優れていると誤って認識されることで、実用時の失敗を招きます。
表面上は素晴らしいモデルに見えても、実際にはノイズを反映しているだけであり、最終的には失敗に終わることが多いのです。
それにもかかわらず、見かけ上の成果により、学界で称賛されたり、商品として人気を博したりすることがあります。

このような間違いは、ランダム性にだまされる人間の性質が原因であり、私たちは間違ったモデルを合理化する理論を作り出し、しばしば自分だけでなく他人をも誤解させます。
マイケル・バビャクが言うように、「科学の世界では好奇心と懐疑心のバランスが求められている」のですが、過剰適合は予測者が好奇心に流される代表的な例です。